From AlphaGo to MuZero
An Introduction to Deepmind’s boardgame AI
Jia-peng Dai
2022/11Contents
AlphaGo (2016)
AlphaGo Zero (2017)
AlphaZero (2018)
MuZero (2020)
From AlphaGo to MuZero
An Introduction to Deepmind’s boardgame AI
Jia-peng Dai
2022/11Contents
AlphaGo (2016)
AlphaGo Zero (2017)
AlphaZero (2018)
MuZero (2020)

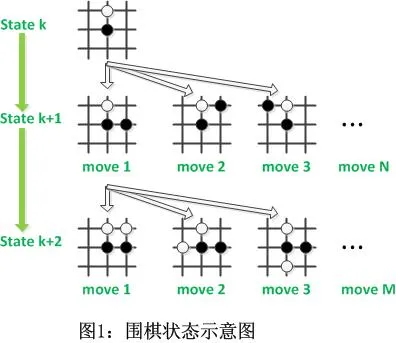
Tree search in Go
Go is a zero-sum game played turn-by-turn on a 19x19 board. The searching process in Go could be perfectly described as a tree search algorithm.
There are theoretically 361! possible situations in a single game. The key to the problem is to reduce the complexity (e.g. Alpha-Beta Pruning, MCTS).
Training pipeline in AlphaGo
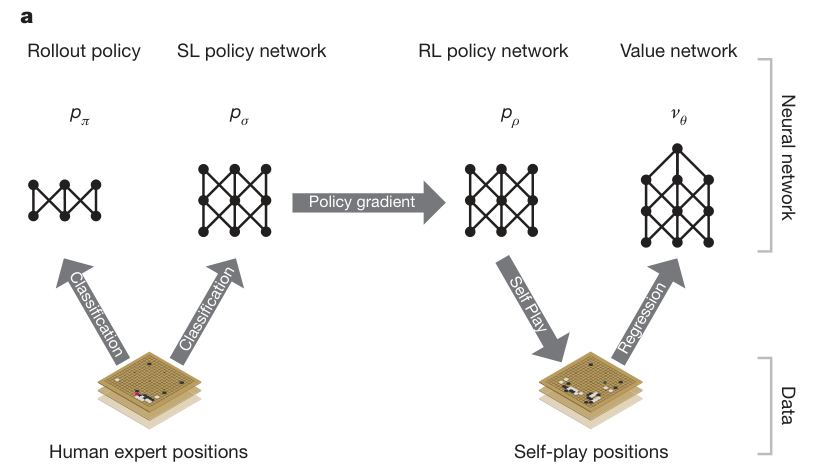
Two-stage training pipeline
Phase 1: Supervised Learning
Train 2 policy networks: Rollout policy & SL policy network.
Learn from human expert positions data to predict the distribution of human expert moves (Classification).
- SL policy network: larger, more accurate but slower. Used in RL stage.
- Rollout policy: smaller, faster but less accurate. Using smaller pattern features. Used in MCTS.
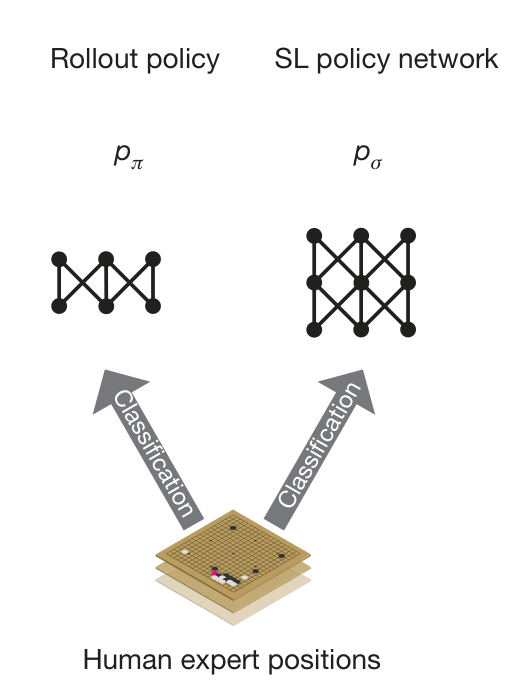
Supervised learning process
Phase 2: Reinforcement Learning
Using Policy Iteration:
Policy improvement (Policy network);
Policy evaluation (Value network).
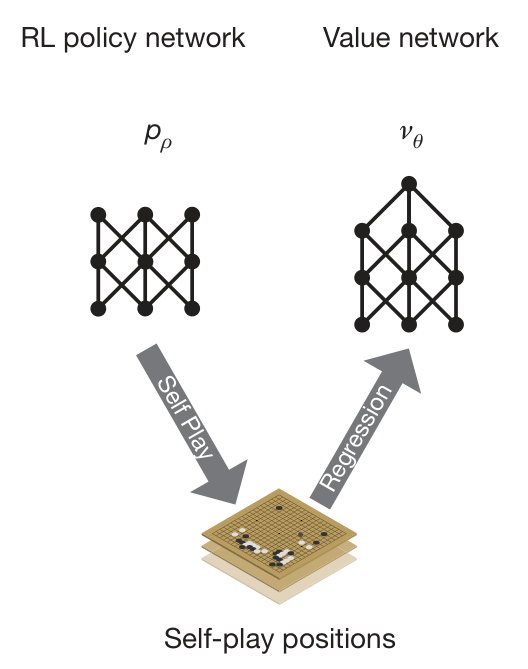
Reinforcement learning process
Phase 2: Reinforcement Learning
Policy network:
initialized as the SL policy network. The output is the action distribution according to the board state.
Self-play: play games between current policy network and a randomly selected previous iteration of the policy network. Stabilize training by preventing overfitting to the current policy.
Every 500 iterations, add the current parameters ρ to the opponent pool.
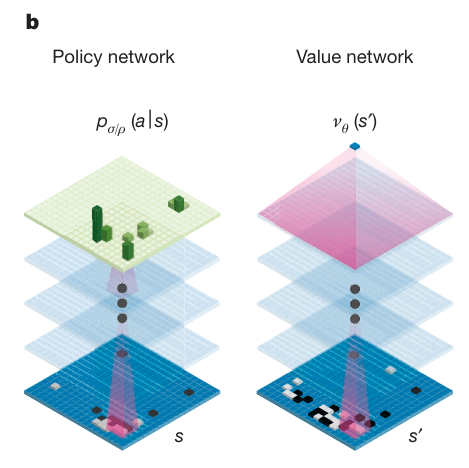
Network Architecture
Phase 2: Reinforcement Learning
Value network:
- estimate a value function vp(s) that predicts the outcome z=±1 from positions of games played by using policy p for both players (Regression).
vp=E[zt∣st=s,at…T∼p]
- zt=±1 is the terminal reward at the end of the game from the perspective of the current player at time step t. Estimated by the MCTS.

Network Architecture
Neural Network Architecture
- 13-layer CNN
- input feature/state size: 19x19x48
- The rules of Go are invariant under rotation and reflection. AlphaGo exploits this symmetrics by passing a mini-batch of all 8 positions into the policy network or value network and computed in parallel.
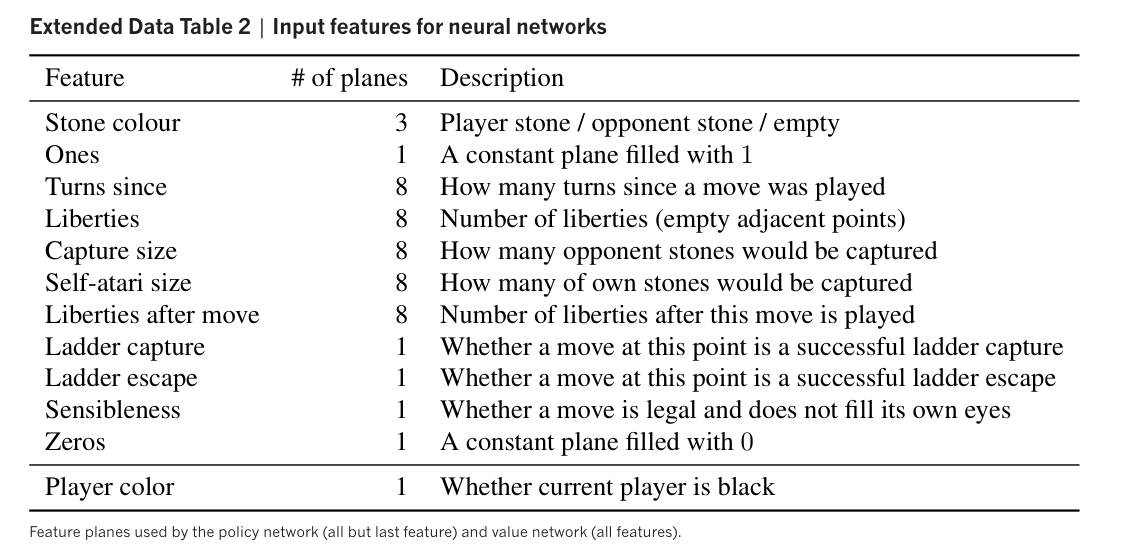
Monte Carlo tree search (MCTS) in AlphaGo
- Monte Carlo method: uses random sampling to estimate the expected outcomes for deterministic problems.
MCTS is used to simulate potential actions to the best results without traversing every node in the search tree.
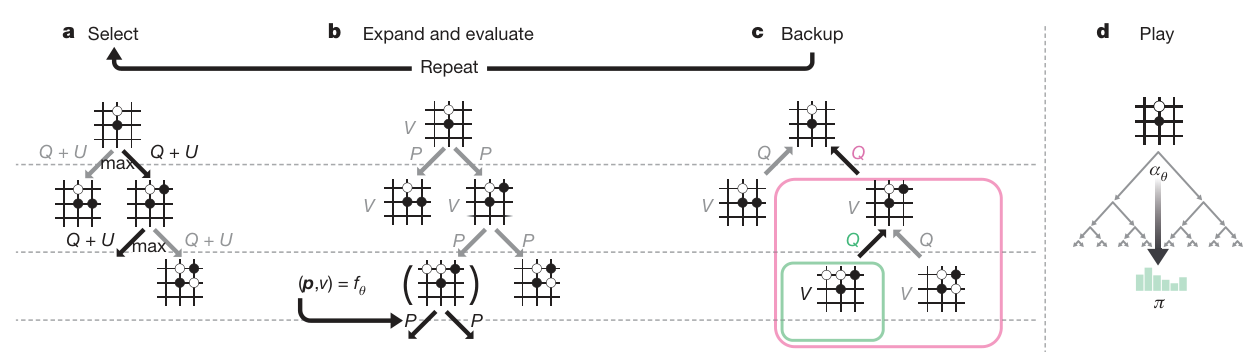
Step 1: Selection
Each simulation starts from the root node to the leaf node (unvisited, non-terminal node).
at=aargmax(Q(st,a)+u(st,a))
u(s,a)∝1+N(s,a)P(s,a)
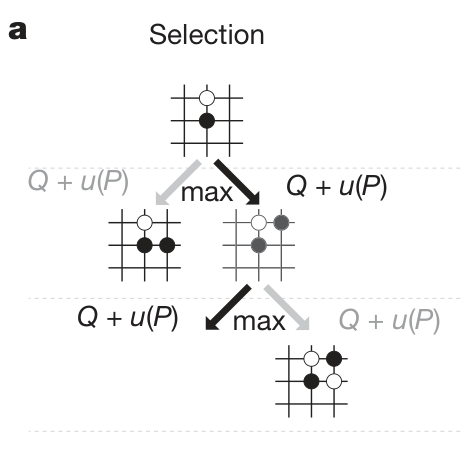
MCTS selection
Step 2: Expansion
When visiting to a leaf node, add new node to the search tree.
Store the prior probability of the node.
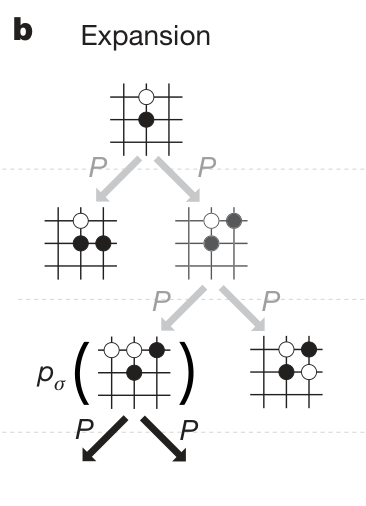
MCTS expansion
Step 3: Evaluation
The leaf node is evaluated in two ways:
by the Value network vθ(sL)
by the outcome zL=±1 of a random rollout until terminal step using the fast rollout policy pπ.
V(sL)=(1−λ)vθ(sL)+λzL
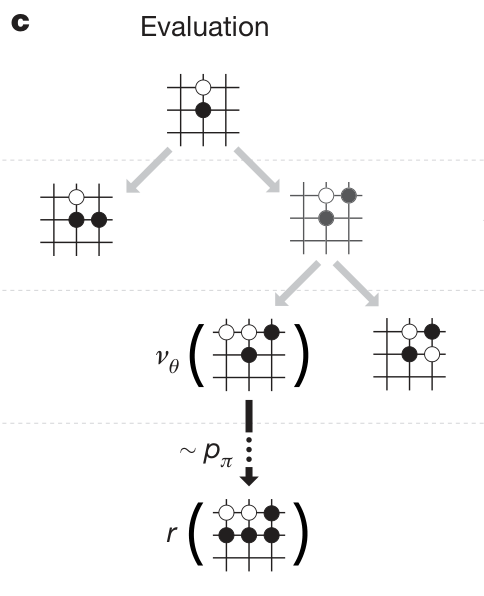
MCTS evaluation
Step 4: Backup
At the end of simulation, the action values and visit counts of all traversed edges are updated.
N(s,a)=i=1∑N1(s,a,i)
Q(s,a)=N(s,a)1i=1∑N1(s,a,i)V(sLi)
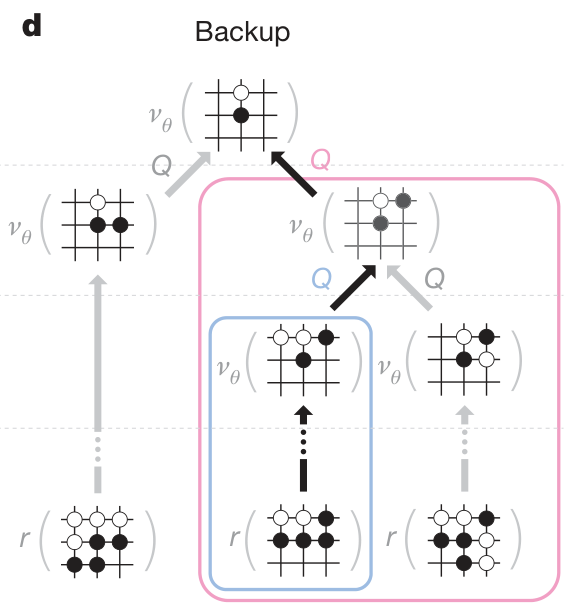
MCTS backup
Training target
- Rollout policy network & SL policy network: maximize the likelihood of the human move a selected in state s.
Δσ∝∂σ∂logPσ(a∣s)
- RL policy network: maximize the expected outcome of the selected move.
Δρ∝∂ρ∂logPρ(a∣s)zt
- Value network: minimize the mean squared error (MSE) between the predicted value vθ(s), and the corresponding outcome z.
Δθ∝∂θ∂vθ(s)(z−vθ(s))
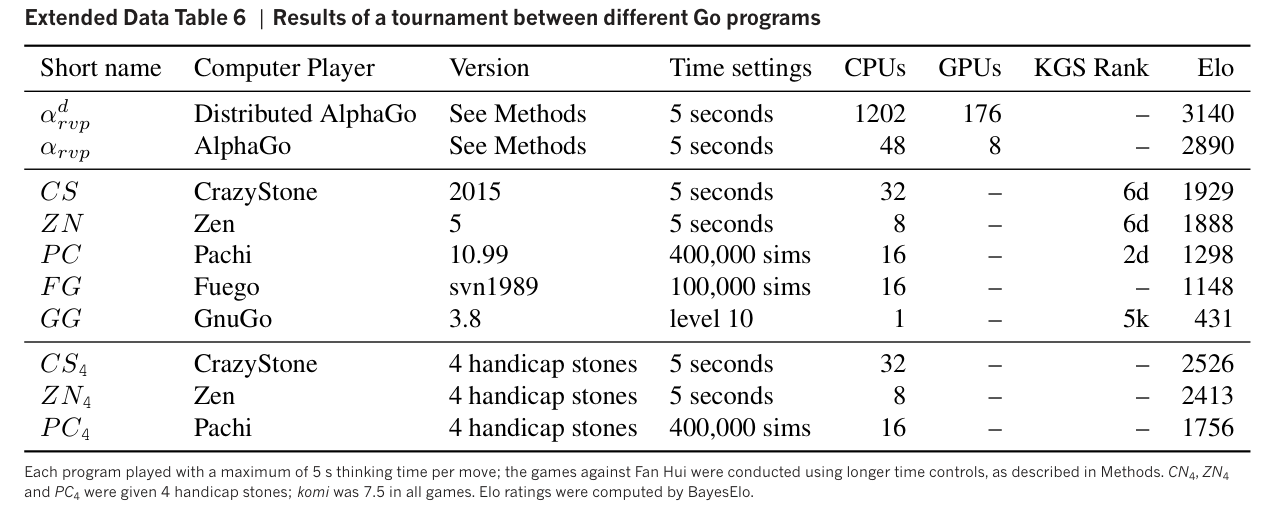
Results
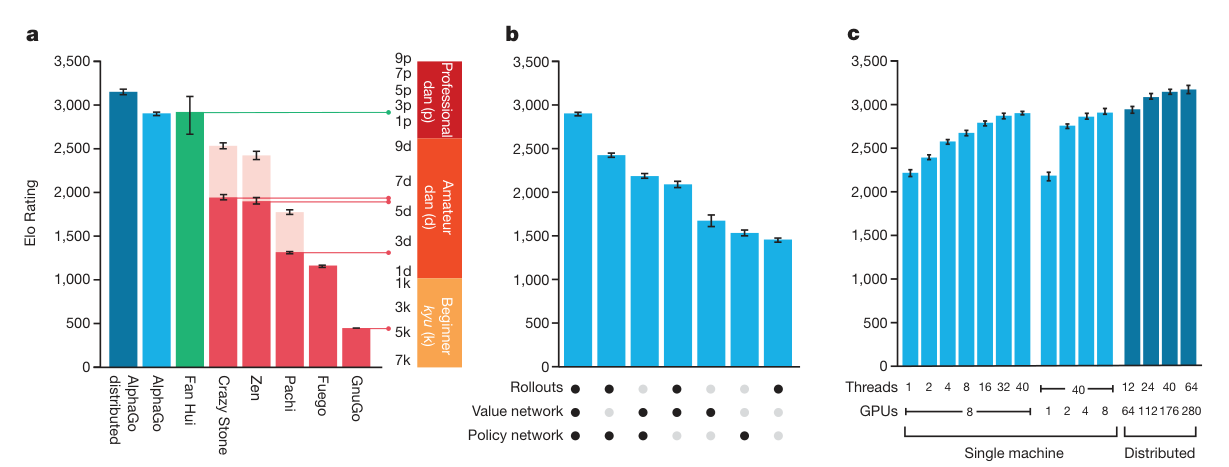
AlphaGo won Fan Hui, the winner of 2013, 2014 and 2015 European Go championships, by 5:0 in a formal five-game match over 5-9 October 2015.
Computing Expenses
- Rollout policy (MCTS): approximately 1,000 simulations per second per CPU thread on an empty board.
- SL policy classification: around 3 weeks for 340 million training steps, using 50 GPUs.
- RL policy network: trained for 10,000 mini-batches of 128 games, using 50 GPUs, for one day.
- Value network: trained for 50 million mini-batches of 32 positions, using 50 GPUs, for one week.
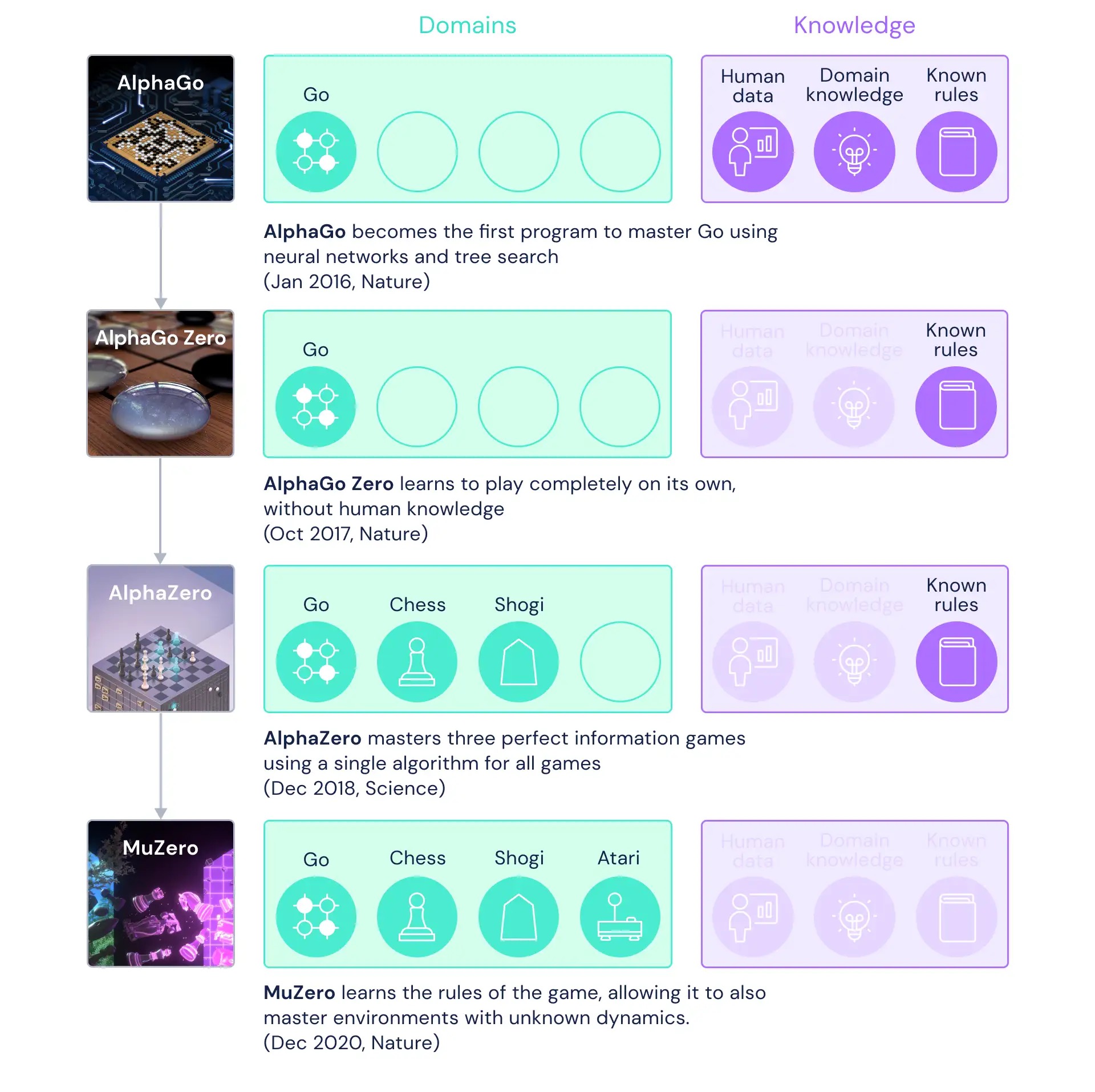
How does it differ from AlphaGo?
AlphaGo Zero is trained solely by self-play, without any supervision or use of human data.
AlphaGo Zero only uses the black and white stones from the Go board as its input.
AlphaGo Zero uses a single neural network, rather than separate policy and value networks.
AlphaGo Zero does not use “rollouts” to evaluate positions and sample moves. Instead, it uses a simpler tree search that relies upon this single neural network.
Self-play training pipeline
A game terminates when both players pass, when the search value drops below a resignation threshold or when the game exceeds a maximum length.
After each iteration of training, the performance of the new player was measured against the best player; if the new player won by a margin of 55%, then it replaced the best player
zt=±1
(p,v)=fθ(s)
l=(z−v)2−πTlogp+c∣∣θ∣∣2
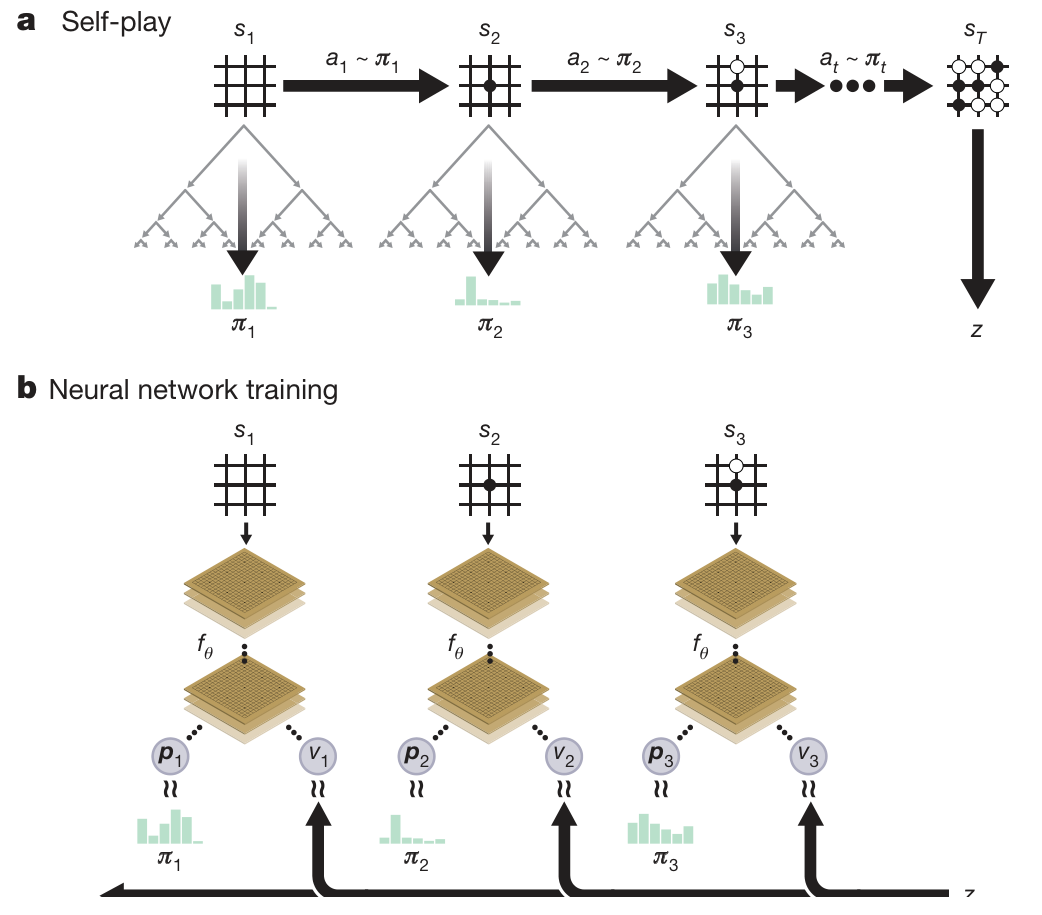
Self-training pipeline
MCTS in AlphaGo Zero
Basically the same as AlphaGo. Sightly different in evaluate and play phase.
- Evaluate: Without random rollouts as in AlphaGo, the action value V(s) of the node s are fully evaluated by the neural network.
(P(s,⋅),V(s))=fθ(s)
- Play: Once the search is complete, search probabilities π are returned, proportional to N1/τ.
- N: the visit count of each move from the root state.
- τ: temperature param that controls the level of exploration. (τ=0: greedy search; τ→∞: uniform sample)
π(a∣s0)=∑bN(s0,b)1/τN(s0,a)1/τ
- the child node corresponding to the played action becomes the new root node; retain the subtree below this child, discard the remainder.
Network Architecture
1 convolutional block followed by 19 or 39 residual block.
- Conv block: conv → BN → relu
- Res block: conv → BN → relu → conv → BN → skip-connect → relu
Two output heads for computing the policy and value.
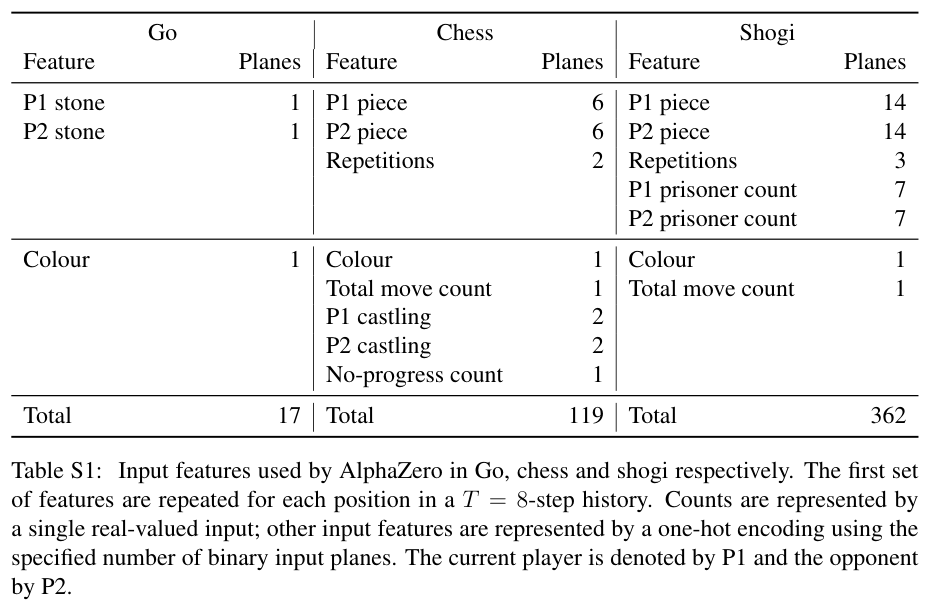
Feature size: 19×19×17 (8 stone history x 2 player existence + 1 color), no hand-crafted features as in AlphaGo.
st=[Xt,Yt,Xt−1,Yt−1,…,Xt−7,Yt−7,C]
- Similar to AlphaGo, AlphaGo Zero also augments the training dataset by sampling random rotations or reflections of the positions during MCTS.
Results
Performance of AlphaGo Zero
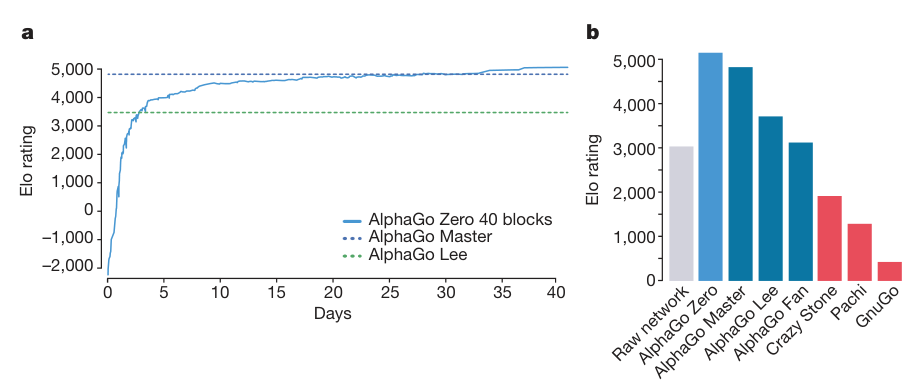
AlphaGo Zero used a single machine with 4 tensor processing units (TPUs), whereas AlphaGo Lee was distributed over many machines and used 48 TPUs. AlphaGo Zero defeated AlphaGo Lee by 100 games to 0.
Results
Network Architecture comparison
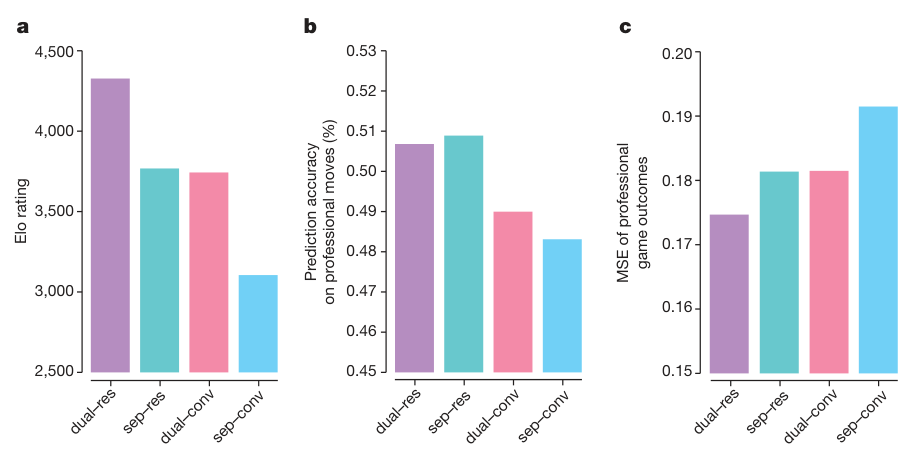
- sep / dual: seperate/combined policy and value networks.
- dual-res and sep-conv correspond to the networks used in AlphaGo Zero and AlphaGo Lee, respectively.
Results
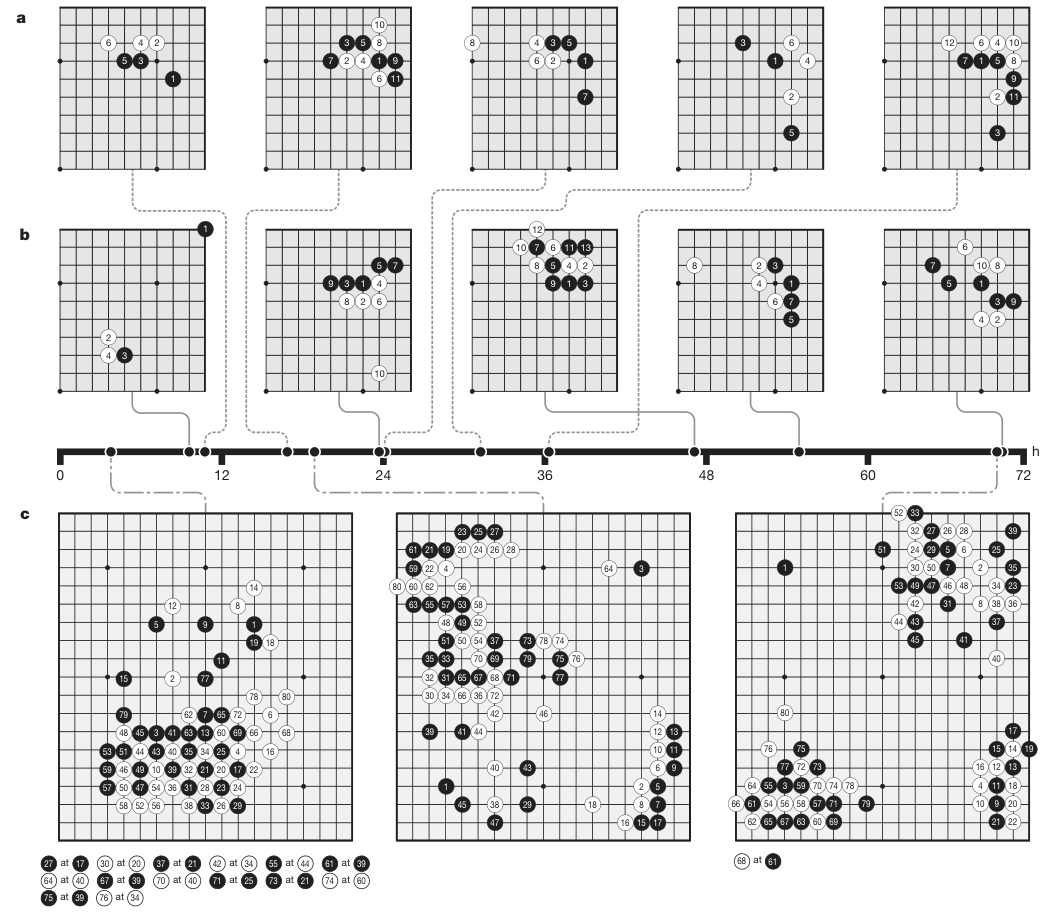
Go knowledge learned by AlphaGo Zero
a: Five human joseki (common corner sequences) discovered during AlphaGo Zero training.
b: Five joseki favoured at different stages of self-play training.
c: The first 80 moves of three selfplay games that were played at different stages of training.
How does it extend AlphaGo Zero?
A more generic version of the AlphaGo Zero that accommodates, without special casing, a broader class of game rules.
Use the same algorithm, network architecture and hyperparameters for chess and shogi, as well as Go.
Go games have a binary win or loss outcome, whereas both chess and shogi may end in drawn outcomes. The game outcome is z={0,±1}: -1 for loss, 0 for draw, 1 for win.
To accommodate a broader class of games, AlphaZero does not assume symmetry. AlphaZero does not augment the training data and does not transform the board position during MCTS.
AlphaZero always generate self-play games with the newest player of last iteration, instead of the best player from all previous iterations as in AlphaGo Zero.
State Representation
feature size: N×N×(MT+L):
N×N represents the board size.
T represents the board positions history at time steps [t−T+1,…,t].
M represents the presence of player’s pieces.
L denotes the player’s color, the move number and other states of special rules.
Illegal moves are masked out by setting their probabilities to zero, and re-normalising the probabilities over the remaining set of legal moves.
Method overwiew
The self-play training process and the neural network architecture (1 Conv block + 19 Res block) are basically the same as AlphaGo Zero.
zt=±1,0
(p,v)=fθ(s)
l=(z−v)2−πTlogp+c∣∣θ∣∣2

Self-play training process in AlphaGo Zero.
Results
Performance
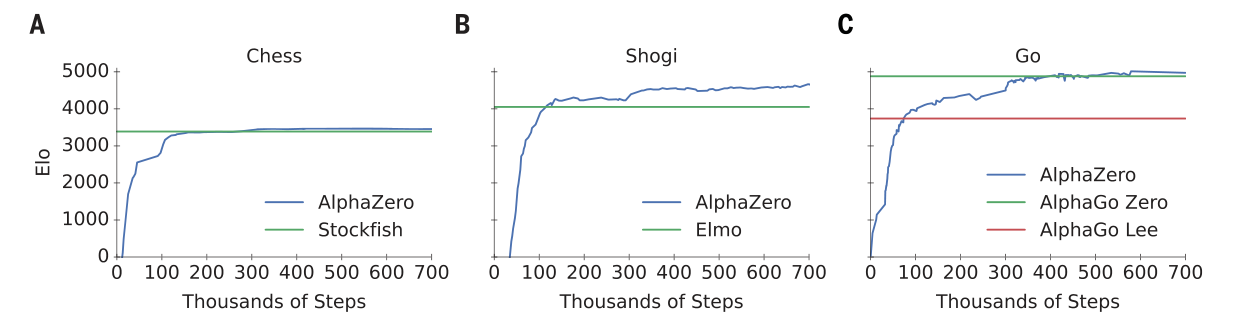
AlphaZero used a single machine with 4 TPUs (same as AlphaGo Zero). Milestones:
- chess: 4 hours (300,000 steps) against Stockfish;
- shogi: 2 hours (110,000 steps) against Elmo;
- Go: 30 hours (74,000 steps) against AlphaGo Lee.
Results
Comparison with specialized programs

What’s different?
MuZero extends AlphaZero to a broader set of environments (e.g. Atari2600), including single agent domains and non-zero rewards at intermediate time steps.
No rules were given in advance, MuZero learned the rules by its internal networks.
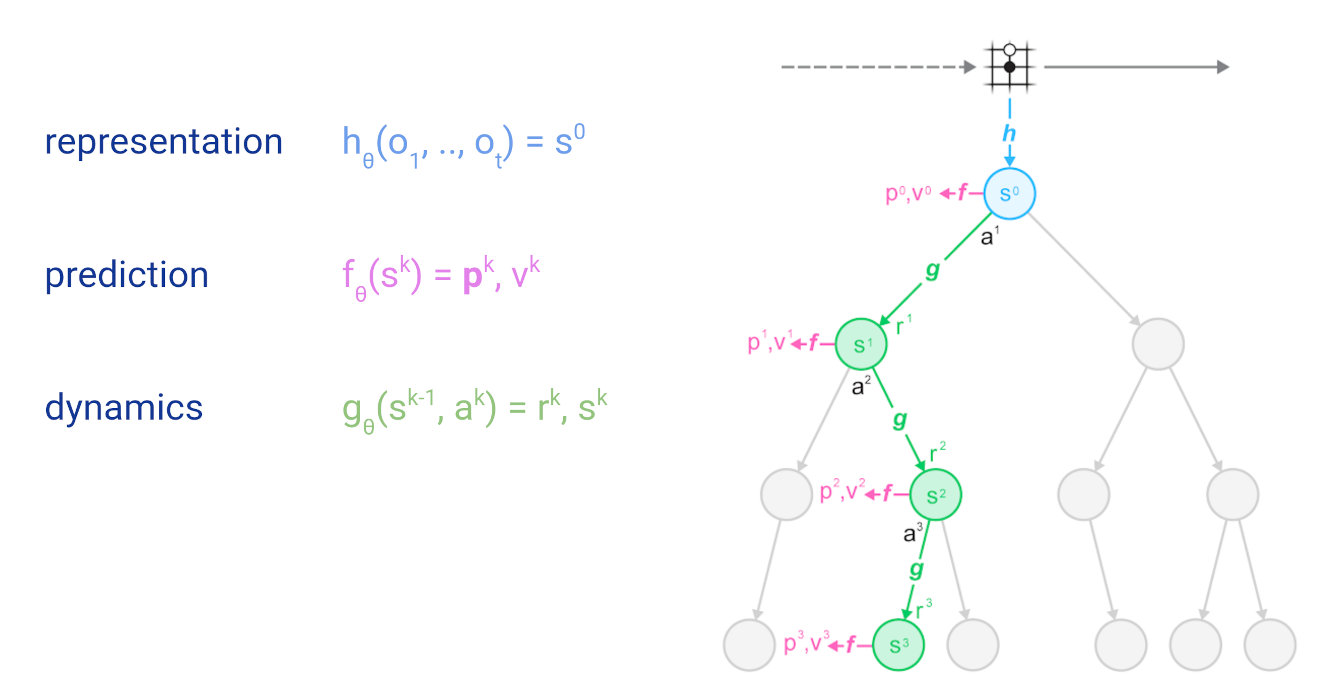
- State transitions: AlphaZero had access to a perfect simulator of the environment’s state-to-state dynamics. In contrast, MuZero employs a learned dynamics model to estimate the simulator.
- Actions available: AlphaZero used the set of legal actions obtained from the simulator to mask the policy network at interior nodes. MuZero does not perform any masking within the search tree.
- Terminal states: AlphaZero stopped at the terminal states directly provided by the simulator. MuZero does not give special treatment to terminal states and always uses the value predicted by the network.
Training process
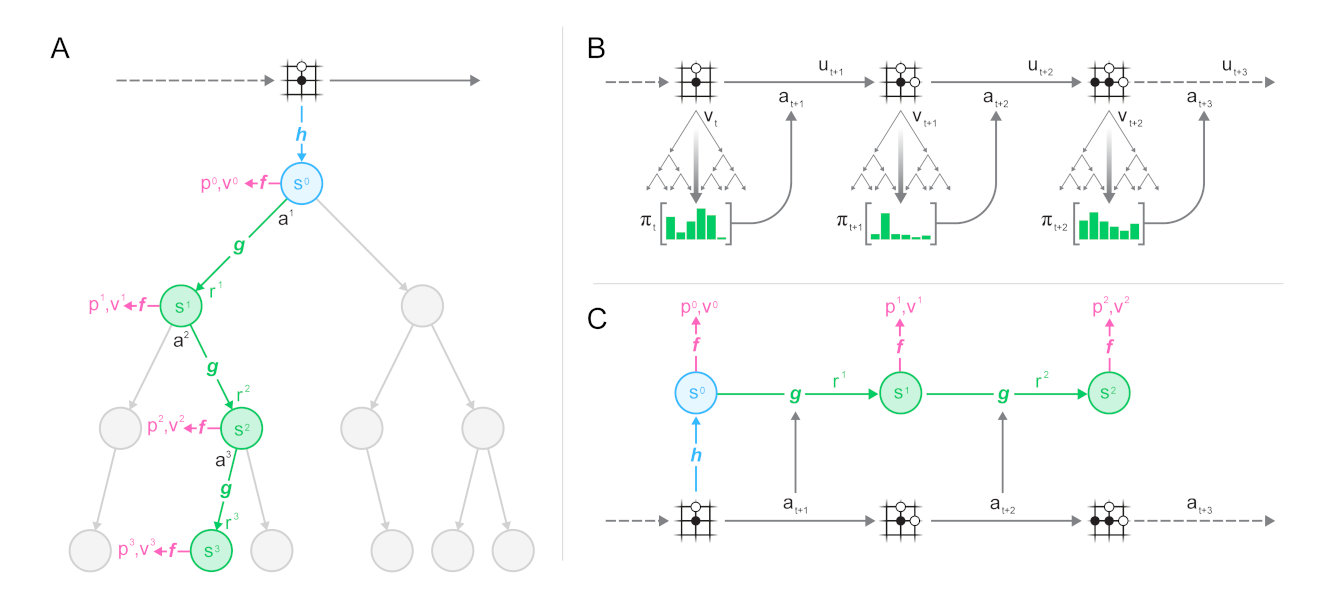
Overall training process of MuZero.
Part 1: MCTS search
Aside from (Q,N,P) as before, the edges in MuZero MCTS also store intermediate reward R(s,a) & state transition S(s,a).
The evaluating value is the k-step cumulative discounted reward:
V(st)=τ=0∑k−1γτrt+τ+γkvt+k
- Because the value above is unbounded, the action-state value Q would be normalized:
Q(s,a)=N(s,a)1i=1∑N1(s,a,i)V(sLi)
Qˉ(s,a)=maxQ−minQQ(s,a)−minQ
Part 2: Self-play process
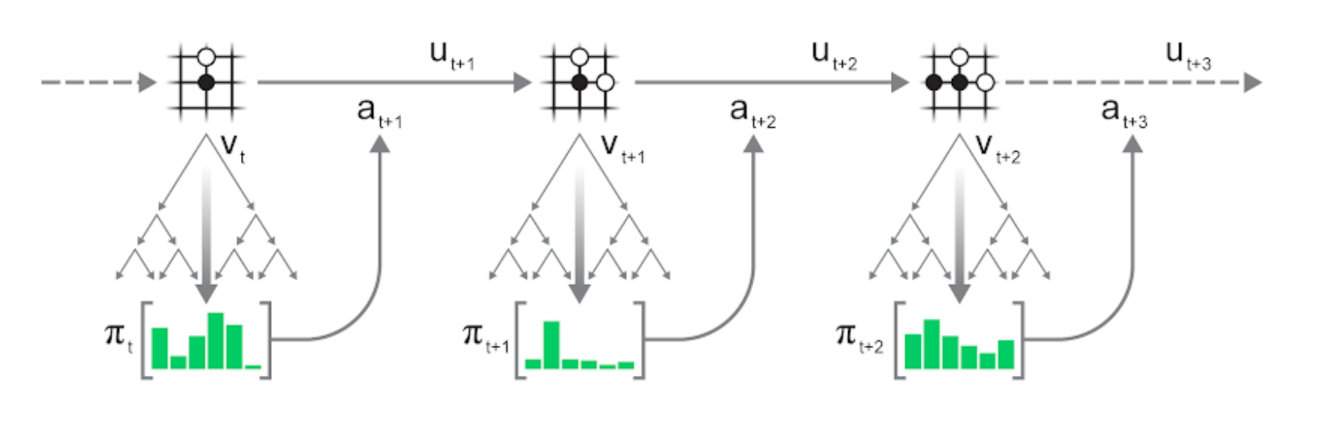
Self-play process is basically the same, except intermediate rewards ut are considered.
The trajectories of self-play would be stored into a replay buffer (off-policy RL).
The final outcome zt is computed as the cumulative discounted reward:
zt=ut+1+γut+2+⋯+γn−1ut+n+γnvt+n
Part 3: Network training
A trajectory is sampled from the replay buffer.
- The representation function h generate the first hidden state representation s0.
- The dynamics function g recursively predicts subsequent rewards rt and states st based on the predicted state st−1 and the real action at.
- The prediction function f predicts the distribution pt and value vt for these predicted states.
- Train the model by minimizing the loss.
l=(z−v)2−πtlogp+(u−r)2+c∣∣θ∣∣2
The network architecture is basically the same as in AlphaZero, but with 16 instead of 20 residual blocks in representation and dynamics networks.
Reanalyze
MuZero Reanalyze revisits its past time steps and re-executes MCTS search using the latest model parameters, potentially resulting in a better-quality policy than the original search.
- This fresh policy is used as the policy target for 80% of updates during MuZero training.
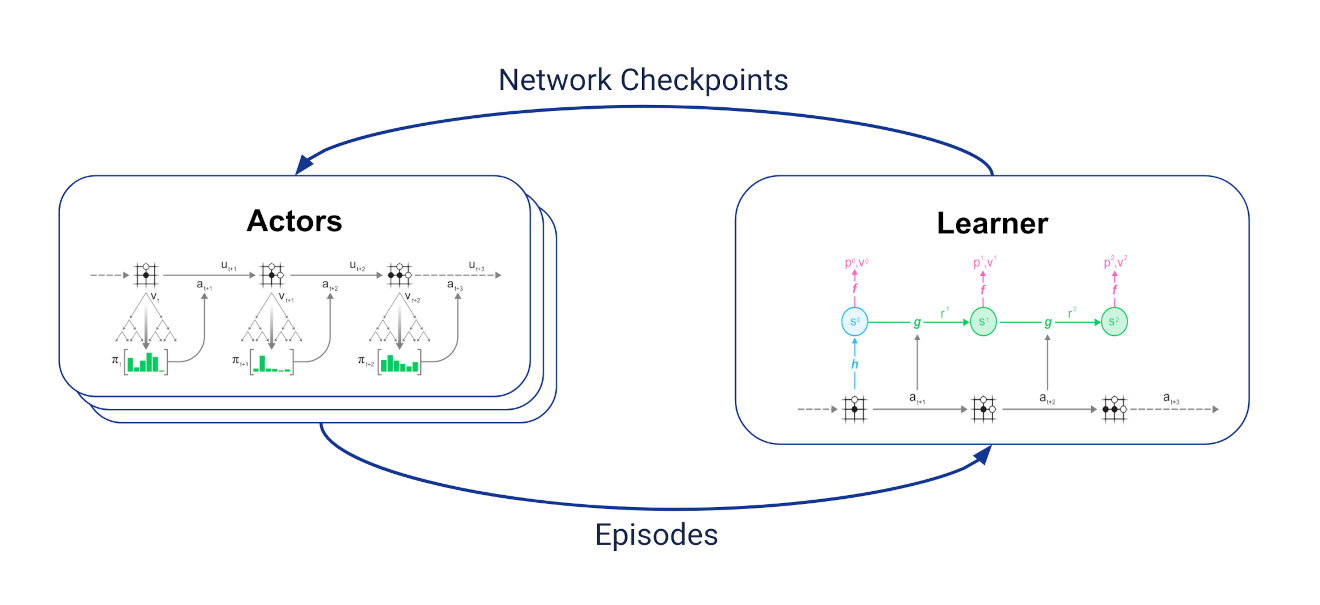
Normal training loop.
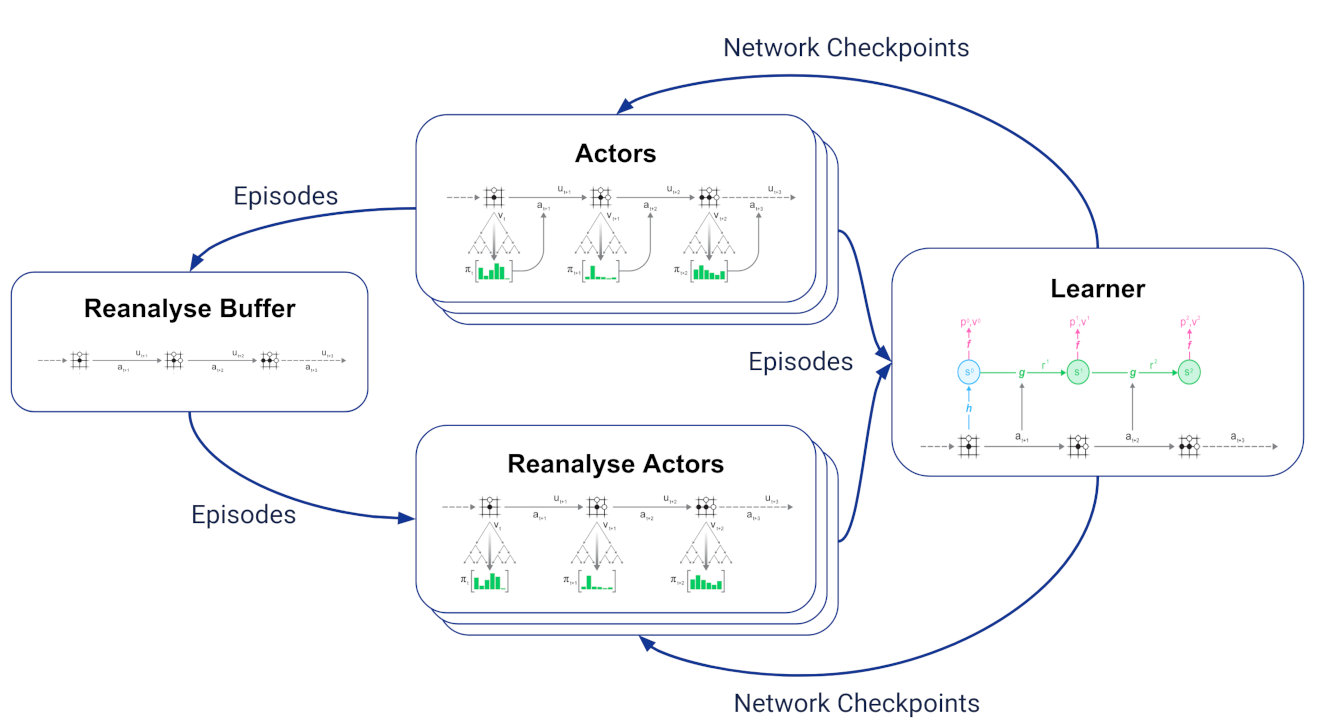
Reanalyze training loop.
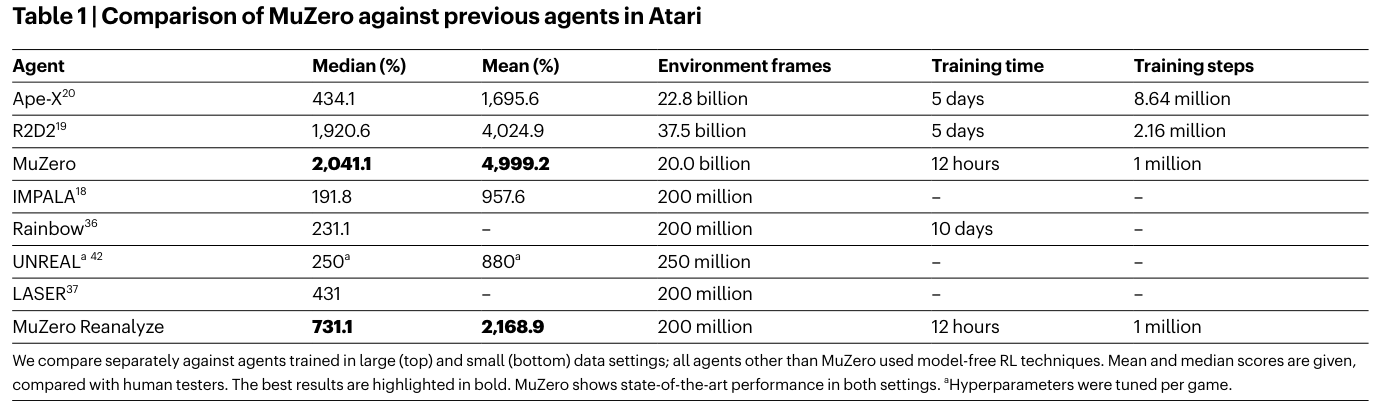
Results
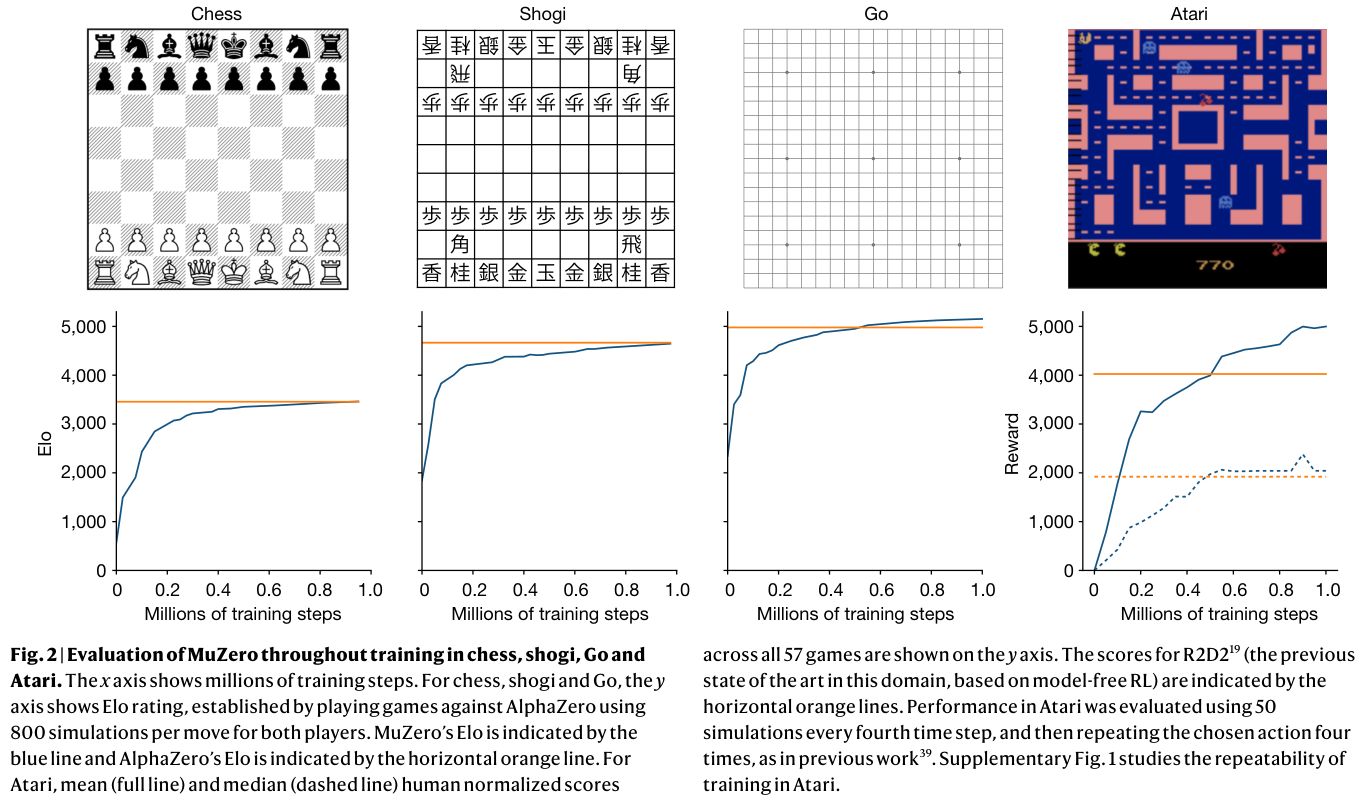
Results
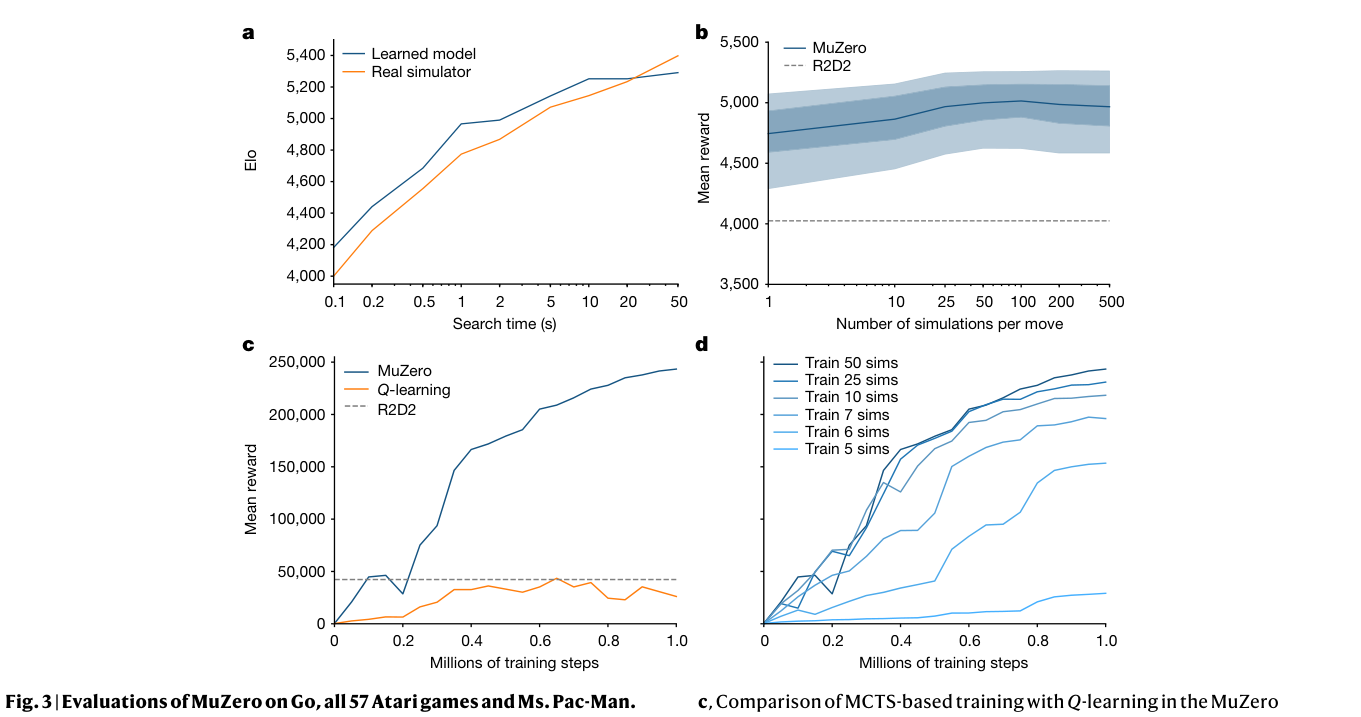
Results
Resources
- AlphaGo (2016): Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. nature, 2016, 529(7587): 484-489.
- AlphaGo Zero (2017): Silver D, Schrittwieser J, Simonyan K, et al. Mastering the game of go without human knowledge[J]. nature, 2017, 550(7676): 354-359.
- AlphaZero (2018): Silver D, Hubert T, Schrittwieser J, et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play[J]. Science, 2018, 362(6419): 1140-1144.
- MuZero (2020): Schrittwieser J, Antonoglou I, Hubert T, et al. Mastering atari, go, chess and shogi by planning with a learned model[J]. Nature, 2020, 588(7839): 604-609.